Tangent Circles

By

Brandon Samples

We begin with the following question. Suppose we start with two circles and a point P on one of the circles. Can we construct a circle which is tangent to both circles with the point of tangency being the point on one of the circles that we started with?

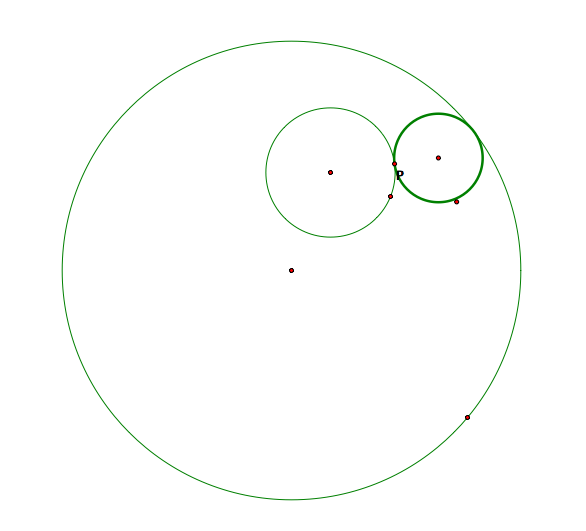
Let's begin by understanding the construction. First start with the two circles and the chosen point P. Let C1 denote the circle containing point P and let C2 denote the other circle that does not contain P. Now, construct a line L through the center of C1 through P and construct a circle with center P that has radius equal to that of C2. Now, form a segment from the intersection point on L furthest from the center of C1 to the center of C2. This forms the base of an isoceles triangle. The center of the desired circle tanget to C1 and C2 at P is precisely the third corner point of this isoceles triangle. The construction is shown in the following figure:

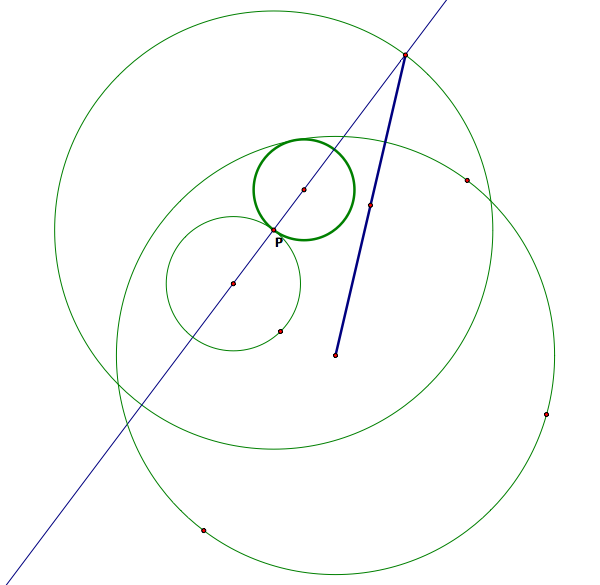
Would you like to see a GSP file of this? GSP File

Now the obvious question that follows is: Have we found all such tangent circles? What about finding the circle which is tangent to both C1 and C2, passes through P, but surrounds one or both of the given circles? Does this have something to do with the our choosing the point of L furthest from the center of C1 rather than choosing the point of L closest to the center of C1? Let's begin by looking at what this construction gives us.

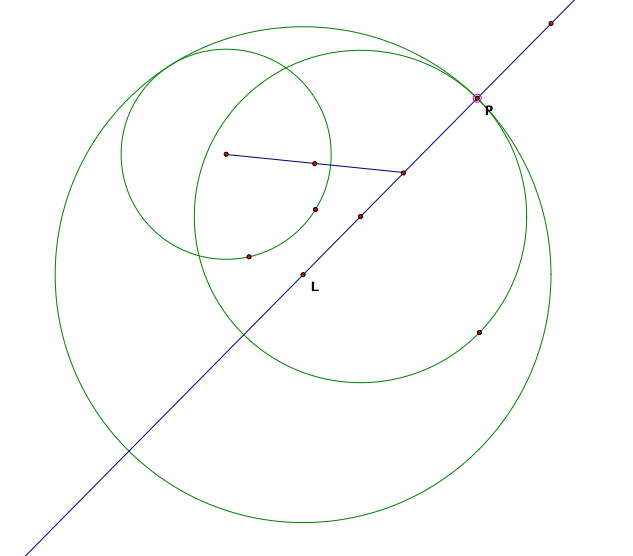
Would you like to see a GSP file of this? GSP File

Now, what happens when we trace the locus of the center of the desired tangent circle? What should we expect? Let's trace the locus in the first case when one circle is contained completely inside the other.

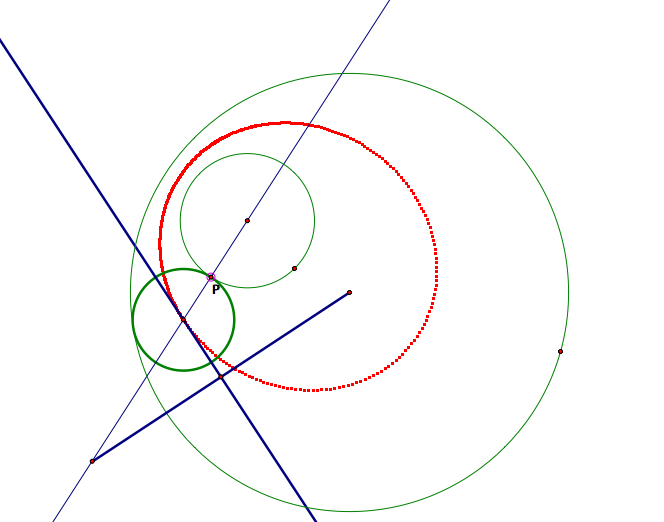
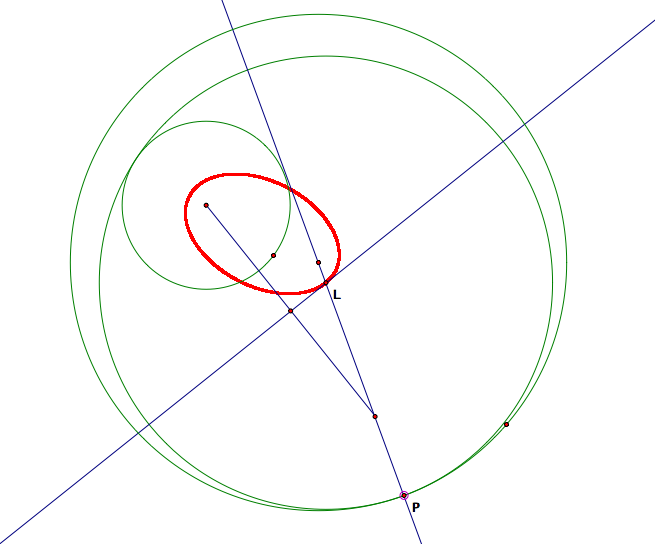
Will it always be an elipse? What about the case when the circles intersect?

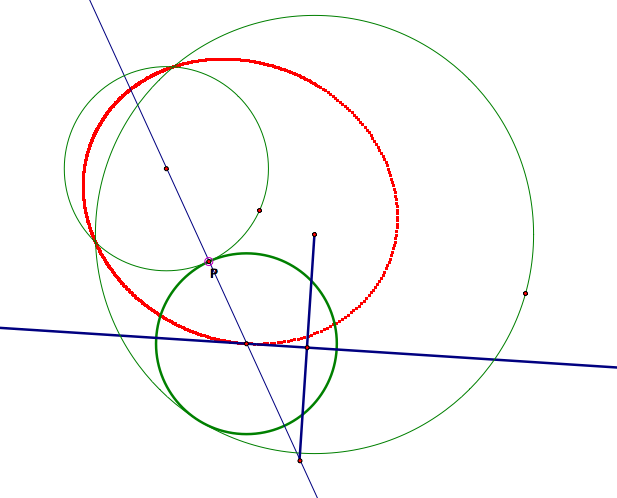
Now, should we expect the locus to be the same for the other construction?

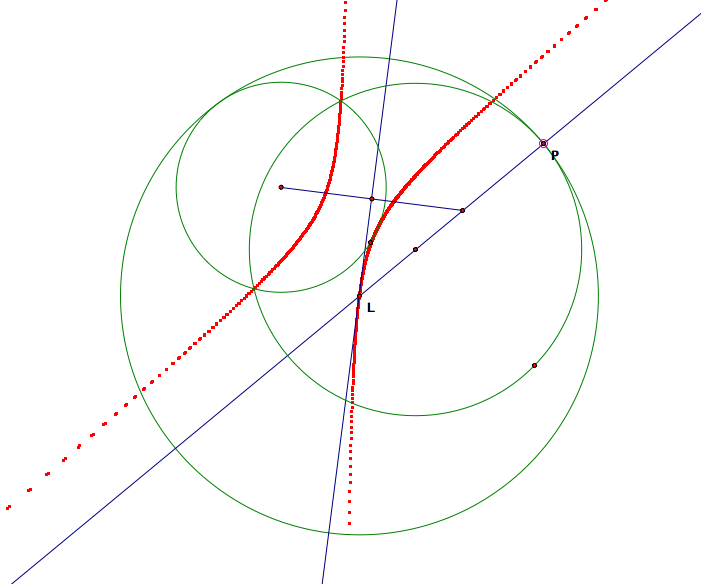
Hmmmm....so what happened? Evidently, the locus forms a hyperbola, which is emphasized by the fact that the tangent circle must get arbitrarily large in order to be tangent to both circles. Now, let's consider the final case when the circles are disjoint.